* All email addresses end with "tohoku.ac.jp".
Akihiro Munemasa
Professor
munemasa@
Yuanyuan Bao
Associate Professor
yybao@
(A01-1) Munemasa Lab conducts research on mathematical theory with algebraic or discrete approach. The following are our main research subjects.
The theory of association schemes has been developed to unify the application of linear programming to coding theory and design theory by Delsarte in 1970's. It generalizes the action of finite groups, and gives a framework for algebraic graph theory, algebraic coding theory and combinatorial design theory. In order to develop algebraic tools for these theories, we investigate applications of algebraic methods to combinatorics, mainly from graph spectra, finite groups, representation theory, linear algebra and optimization.
A code is a subspace of a finite-dimensional vector space over a finite field. This seemingly simple concept has been widely used to study combinatorial problems using algebraic methods. Codes themselves can also be investigated from tools in number theory, modular forms in particular, via integral lattices. The class of self-dual codes is an interesting class of codes which give rise to unimodular lattices, and are related to the sphere packing problem. Moreover, some vertex operator algebras are constructed from codes and lattices. We investigate the problems of construction and classification of codes and lattices and study their relations.
The research field of (A01-2) Bao Lab is low-dimensional Topology. We study closed curves and graphs in 3-dimensional space (which are called knots and spatial graphs), and 3-dim manifolds.
For a simple closed curve on the plane, Jordan-Schönflies theorem states that it always bounds a disk. But when we consider a simple closed curve in the 3-dim space, it may not bound a disk. The curves in Fig (a)(b) bound disks but the curves in Fig (c)(d) don’t. Therefore, studying how a curve is knotted in the 3-dim space becomes a non-trivial question.
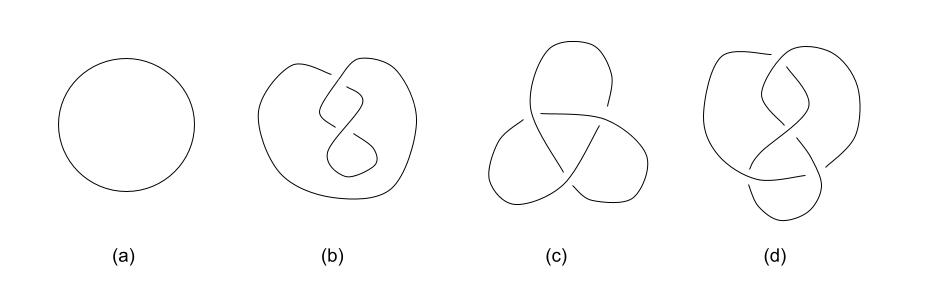
The curves mentioned above are called knots. If one knot can transform itself to another knot withing cutting itself (I always think a knot is a living thing), we identify them and call them equivalent knots. A knot bounding a disk is always equivalent to the circle in Fig(a). The knots in Fig(c)(d) are not equivalent to each other. In knot theory, we study the topological properties of knots under this equivalent relation.
In modern knot theory, many mathematical ideas, such as from algebra and analysis, are utilized in the study of knots. Here I introduce several methods that are used in the study of knots.
We can use algebraic topology to study knots. The knot complement, which is a 3-dim manifold with boundary, is obtained by removing an open tubular neighborhood of a knot. The knot group is defined to be the fundamental group of the knot complement, and it contains almost all information about the knot. For example, the Alexander polynomial can be calculated from a presentation of the knot group by taking Fox calculus.
From 1980’s, after the discovery of Jones polynomial, a class of new invariants, which are called quantum invariants, are discovered. Roughly speaking, a quantum invariant is defined from a quantum group and its representation. The Alexander polynomial, which is usually regarded as a classical knot invariant (compared to quantum invariant), can also be reconstructed as a quantum invariant.
Around millennium, using techniques in Lagrangian Floer homology, Ozsváth and Szabó constructed Heegaard Floer homology for a 3-dim manifold and for a knot. As topological applications, many new results about knot concordance, unknotting numbers, Dehn surgeries etc. are obtained from this homology.
The embedding of a 1-dim simplicial complex (graph) into the 3-dim space is called a spatial graph. Spatial graphs are an important research subject as an extension of knots, and are also attracting attention as mathematical models for polymer compounds. Given a theory of knots, a natural question is whether this theory can be extended to spatial graphs. For example, quantum invariants can basically be extended from knots to graphs. On the other hand, there are many concepts that cannot be extended well to spatial graphs, such as unknotting numbers and Seifert surfaces of knots.
A Hausdorff topological space with a countable basis that is locally homeomorphic to the 3-dim space is called a 3-dim manifold. There are several ways to construct 3-dim manifolds from knots. In addition to the knot complement space mentioned earlier, there are methods using branched covering and Dehn surgery. Any oriented closed 3-manifold is realized as a covering of the 3-dim sphere branched over a knot (Alexander's theorem). Also, any oriented closed 3-manifold can be obtained by Dehn surgery along a link (Kirby Calculus). Under this relationship, research on knots and research on 3-dim manifolds influence each other deeply.
If you are interested in the research field of our laboratory, please feel free to contact us by email.
The following book explains what a knot is in an easy-to-understand manner. It is aimed at high school students, so you can read it without any prior knowledge. Please try solving the practice problems and see if knots are interesting to you.
The following two books are recommended for fourth-year undergraduate students and first-year master's students who want to study knot theory.
Toshiyuki Sugawa
Professor
sugawa@math.is.
The research subject of (A02-1) Sugawa Labo is mainly Complex Analysis.
Even if the data and/or functions are described in terms of real variables, hidden structures may emerge when dealing with them as complex variables. For instance, in the classical problems of moments concerning a sequence of real numbers, the power series formed by the sequence (the generating function) gives us many useful visions to tackle the problems. In such a case, Complex Analysis plays an important role. We are studying analytic functions from the geometric view-point to provide new interpretations to classical results. Moreover, we are interested in quasiconformal mappings, which have recently found many applications in image processing and brain mapping. With the help of computers together with the above knowledge, we are studying modern topics such as Teichmueller spaces, Kleinian groups, Complex Dynamics, and fractals, as well.
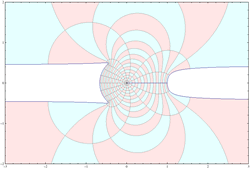
[The image of the unit disk $|z|<1$ under the conformal mapping $f(z)=z(2-z+z^2)/(2-2z+2z^2)$]
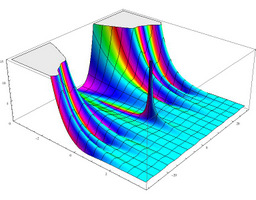
[A graph of the Riemann zeta function: the height means the absolute value and the color means the argument.]
Hajime Tanaka
Professor
htanaka@
Tanaka Lab studies various combinatorial objects, mainly by means of algebraic methods.
Homogeneous spaces of finite groups, and Gelfand pairs in particular, have been an active area of research, (partly) because of their connections to, and/or importance in, number theory, orthogonal polynomials and random walks, just to name a few. However, it often turns out to be quite important and natural to shift from "group symmetry" to "combinatorial regularity", and this leads us to the concept of association schemes, which was originally introduced in the design of statistical experiments. We study Gelfand pairs and association schemes through the representations and characters (i.e., spherical functions) of the associated commutative semisimple $\mathbb{C}$-algebras (Hecke algebras and Bose-Mesner algebras), and explore their applications further.
Distance-regular graphs are finite simple graphs with certain very strong combinatorial regularity. They form a special subclass of association schemes corresponding to two-point homogeneous spaces. Distance-regular graphs are also used as test instances for problems on general graphs, such as random walks and combinatorial optimization. We study distance-regular graphs, in particular their Terwilliger algebras, which are noncommutative semisimple $\mathbb{C}$-algebra introduced by Paul Terwilliger in the early 1990s. Our subjects also include general algebraic/spectral graph theory.
Various combinatorial objects, including codes and designs, can be viewed as certain subsets of the vertex sets of association schemes and distance-regular graphs. In his monumental thesis in 1973, Philippe Delsarte combined linear programming with the representation theory of the Bose-Mesner algebra to establish a unified theory to study these combinatorial objects, which continues to play a central role in algebraic combinatorics. One of our projects on this topic aims to extend Delsarte's theory based on semidefinite programming and the Terwilliger algebra.
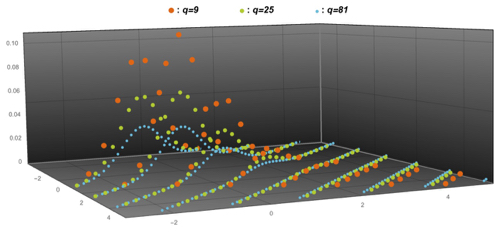
[Normalized joint spectral distributions of Cartesian powers of Paley graphs $\mathrm{Paley}(q)$ and their complements]
You are welcome to contact me by email if you are interested in the above topics, or more generally, "algebra and combinatorics". The following is a list of (recent) books related to our research:
Hiromi Seno
Professor
seno.math.is@
Seno Labo focuses the theoretical study of mathematical modeling for biological/social phenomena, and the theory on the mathematial structure of modeling.
Mathematical biology is an interdisciplinary field growing in a wide range between mathematical and life sciences. Essential theories of mathematics and physics are applied for mathematical analysis in this field. Their development promotes the application of mathematical and theoretical approach for various biological phenomena. Even if the research subject is hard to be attacked with field observation or laboratory experiment, thought experiment could be useful to get some perspectives to conduct field observation or laboratory experiment. Analysis of mathematical model for some problem of theoretical biology can contribute to the systemization of biological theory, and would bring a cue for new biological research. Theory of chaos is one of examples that model analysis in mathematical biology contributed to the development of theories in mathematics and physics.
Principal subject of our study is the mathematical model analysis to make clear or present the point at issue for scientific discussion about real biological/social phenomena, or to promote the advanced theoretical research. Model as simple as possible with only essential factors selected for the targeted phenomenon would provide with scientific (qualitative) discussion about it. Theory of basic modeling could contribute to more advanced modeling for concrete problem about real phenomena. Theoretical research with mathematical model plays an important role for the systemization of biological/social theory.
Focal points in the study of our labo are what theoretical problem about target phenomenon is treated, how the problem is mathematically modeled, what mathematical analysis is applied for the model, how the mathematical result is lead to the discussion in biological/social science. Especially we focus the modeling of mathematical model as simple as possible, which could grasp the nature of phenomenon, and we study the rational consistency/adaptability of mathematical modeling to assumption/hypothesis about biological/social phenomenon.
Generally speaking, mathematical modeling is the process to construct mathematical model with mathematical expression/translation of assumption/hypothesis about the biological/social phenomenon. Estimation of adaptability or translation of such assumption/hypothesis requires knowledge and sense of biological/social science. On the other side, mathematical expression/translation of them requires mathematical knowledge and sense. Therefore, we need an appropriate integration of them for mathematical modeling. This is an interdisciplinary characteristics of the research with mathematical model that has the rational consistency/adaptability to assumption/hypothesis about real phenomenon.
Seno Labo attacks a variety of theoretical problems about biological/social phenomena in wide range of spatial/temporal scale. Some examples of interested research subjects are
We analyzed basic models which were constructed with application of stochastic process, difference equations, differential equations etc. They were not mainly to be applied for real data analysis, whereas they aimed to make clear the point at scientific issue and to provide some bases of mathematical modeling for advanced/applied researches about real phenomena.
Characteristics of our labo is that we study the mathematical modeling itself as appropriate integration of knowledges and senses in mathematical and biological/social sciences. This can be regarded as an interdisciplinary or applied mathematical viewpoint. Variety of fields or problems contributed by applied mathematics or mathematical biology have been provided from life/social sciences. Researchers with such interdisciplinary mathematical sense shall serve the development in science of coming ages. If you are interested in our labo, please check the web page here to get detail information.
Masaaki Harada
Professor
mharada@
Kei Funano
Associate Professor
kfunano@
Junya Takahashi
Assistant Professor
t-junya@
(B01-1) Harada Lab studies algebraic coding theory, combinatorial design theory and related combinatorial structures.
Our major topic in algebraic coding theory is self-dual codes by an algebraic approach and a combinatorial approach. We are also interested in related combinatorial structures and discrete structures.
Combinatorial designs are one of combinatorial structures. Our major topics in combinatorial design theory are symmetric designs, $t$-designs and Hadamard matrices by an algebraic approach and a combinatorial approach.
In (B01-2) Funano Lab, we study Riemannian geometry, spectral geometry, geometry of Banach spaces and metric spaces, and their related topics.
There are three notions that describe how much our spaces are curved. These are called, sectional curvature, Ricci curvature, and scalar curvature. It is classical that assuming lower bounds of these curvatures corresponds to comparing our space with a simple model space such as euclidean spheres, euclidean spaces, and hyperbolic spaces in some sense. In comparison geometry we study geometric properties by comparing with these spaces. On the other hand there are two notions, called type and cotype in Banach space geometry. These two notions compare Banach spaces with Euclidean spaces in a different fashion. Recently these notions of comparison has been extended to metric spaces and we can now treat wild spaces. Also various methods and notions in convex geometry has been extended to Riemannian manifolds with lower Ricci curvature bounds and we find a close relation between convex geometry and comparison geometry of Ricci curvature. We could expect further development in comparison geometry.
The Laplacian is the most basic elliptic second differential operator. It appears not only in the theory of PDE but also in geometry in various situations. It is known that solutions of heat equations, wave equations, and Schrödinger equations are expressed in terms of eigenvalues and eigenfunctions of the Laplacian and so it is important to understand eigenvalues and eigenfunctions to have a better understanding of solutions of these equations. Eigenvalues and eigenfunctions of the Laplacian is closely related with geometric quantities, such as curvature, volumes, distributions of closed geodesics etc. In a discrete setting, it is related with construction of efficient and economical networks and clusterings. In recent years I tried to study eigenvalues and eigenfunctions using optimal transport theory and algebraic topology. I'm also interested in another min-max theory, such as widths, waists etc. These are related with geometric measure theory and theory of minimal surfaces.
You are encouraged to send me an email if you have an interest in the above topics and prepare for an entrance examination.
Kanta Naito
Professor
knaito@
Takako Nemoto
Associate Professor
nemototakako@
Have you ever been unsure about what to do when trying to prove a theorem? The proof of mathematical theorems is derived by combining "axioms" and "inferences". Axioms are assumptions which are assumed to be true without proof. For example, the axiom of groups specifies the conditions that a group must satisfy and defines what a group is. "Inferences" are rules that determine what conclusions can be drived from what assumptions. For example, the modus ponens "if A then B", and "A", therefore "B" is one inference rules. In Mathematical logic, logics, proofs, models, sets and computations, which are routinely used inusual mathematics, are objects of analysing. My research aims, in a word, to reveal "what can be concluded when given any axioms and inference rules".
Although we usually don't pay much attention to it, most of the theorems in ordinary mathematics are formalized and proved using the axioms of set theory called ZFC and the inference rules of classical logic. However, this is not the only correct set of axioms and logic. For example, if we build inference rules based on the motivation that a proposition is true if a proof is given, we cannot necessarily conclude "A or not A" for unresolved problems. Even considering proofs written by computers as true leads to the same issue, which becomes a theoretical background for automated theorem proving and proof assistance systems. When we try to do mathematics using different inferences than usual, we can see a world that is quite different from ordinary mathematics, which is very exciting.
Students who have an interest in topics such as proofs, models, sets, and more are welcome, regardless of whether they have studied mathematical logic during their undergraduate studies. Research topics will be tailored to the individual interests of students. If you are interested in studying with me, please feel free to reach out via email.
[A proof of logica principle from the existence of a path of infinite binary trees]
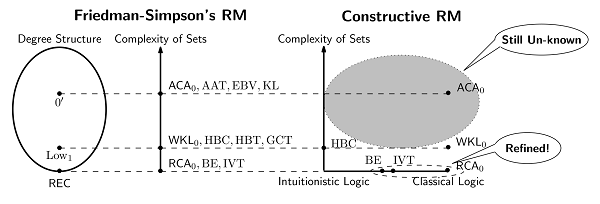
[Classification of mathematical theorems in constructive revese mathematics]
Yuko Araki
Professor
yaraki@
