ホーム > 講演会

講演会

数学と諸分野の協働に関する「講演会」を定期開催し、 研究科内の諸分野と数学の双方向の協働を進める場 および異分野研究者の出会いの場を提供する。

第28回講演会（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2019年03月12日(火) 16:45〜17:30
会場：東北大学 情報科学研究棟 中講義室
講演者：荻原 哲平　氏 (統計数理研究所)
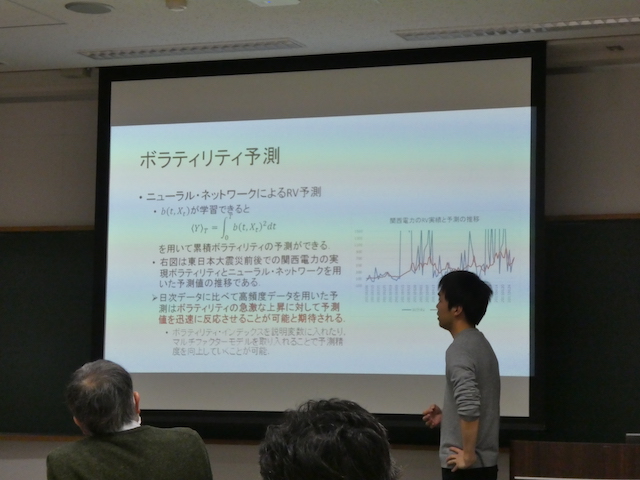
タイトル：高頻度データを用いた株価変動リスクの統計解析とニューラル・ネットワーク
概要：金融機関は保有する株式の株価変動による金融資産価値の変動をコントロールする必要があり，株価データや財務データから統計解析を用いて将来の株価の分散・共分散を予測してリスク・コントロールを行っている．特に年金基金の株式運用やインデックス・ファンドの運用においては株価変動リスクをより正確にコントロールすることが求められ，株価の分散・共分散の高い予測精度が必要となる．近年は株式市場の一日内の全取引を記録したような「高頻度データ」が容易に入手できるようになり，このようなデータを用いた株価変動リスクの計測が活発に研究されている．高頻度データはその情報量の多さからより精度の高い予測が可能になると期待されている一方で，特有の複雑な構造から統計解析に困難が生じる．本講演では，株価を確率過程でモデリングした時の高頻度データの複雑な構造を考慮した統計解析手法を紹介する．また，高頻度データのデータ量を活用してニューラル・ネットワークと上記の統計解析手法を融合して株価構造を学習するアプローチに関しても紹介する．

第27回講演会（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2019年03月12日(火) 16:00〜16:45
会場：東北大学 情報科学研究棟 中講義室
講演者：平井 広志　氏 (東京大学)
タイトル：CAT(0)空間上のアルゴリズムと最適化について
概要：CAT(0)空間と呼ばれるユークリッド空間や双曲空間を一般化した距離空間がある． CAT(0)とは，「曲率が非正」ということを意味している． この空間は，ユークリッド空間で成り立つ様々な良い性質を引き継いでいる． 特に，任意の２点を結ぶ測地線（ = 最短路）が一意に定まる． このことから凸関数なども自然に定義される． 最近になって，CAT(0)空間を利用したモデリングやその上でのアルゴリズム・最適化理論が展開され始めている． たとえば、系統樹のなす空間をCAT(0)空間として実現し、2つの系統樹の中点や、複数の系統樹の重心を計算する試みや、 ある種の変形ロボットの状態空間をCAT(0)空間として実現し、 測地線を計算することより最適動作計画を得る試みがある。 本発表では，そのような試みの一端を紹介する．

第26回講演会（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2019年02月12日(火) 14:00〜15:00
会場：東北大学 情報科学研究棟 中講義室
講演者：持橋　大地　(統計数理研究所)
タイトル：階層Pitman-Yor過程による半教師あり形態素解析
概要：自然言語の単語の頻度分布は一般に巾乗則に従い, それはPitman-Yor過程(Pitman andYor 1997), ある いはそれを階層化した階層Pitman-Yor過程(Teh 2006) とよばれる確率過程によってよく近似できることが知られ ている。このことを利用し, 文字と単語のMarkovモデル にネストされた階層Pitman-Yor言語モデルを考えること で, たとえ未知の言語でも, 生の文字列だけから「単語」 を完全に自動的に推定できる統計モデルを2009年に発表 した(Mochihashi et al. 2009)。しかし, 実際の応用で は人手で構築した単語分割の教師データや辞書が利用でき ることが多く, そうした教師データの情報も利用する半教 師あり学習の必要性がもっとも高いと考えられる。そこで, 形態素解析の教師あり学習のための標準的なモデルである CRF(条件付確率場)と上記の階層Pitman-Yor過程による 言語モデルを接続し, 互いに補い合うことで,教師データに ない未知の言語表現からも適切に「単語」を認識すること のできる半教師あり学習の枠組(Fujii et al. 2016)につ いて解説する。また, 近年のニューラル言語モデルの発展 も踏まえ, 現代的な立場からこうした研究をどう発展させ ていくかについての議論も同時に行いたい。

第25回講演会（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2019年02月05日(月) 15:00〜16:00
会場：東北大学 情報科学研究棟 大講義室
講演者：林 正人 (名古屋大学)
タイトル：測定型量子計算による量子計算の検証
概要：量子計算はこれまでの従来型の古典計算機の性能を上回るものとして，期待されている．しかしながら，できあがった量子計算機の構成要素にエラーがあると，正しい計算結果は得られない．そのため，量子計算機が正しく実装されているか検証することは，実用上不可欠である．計算したい問題がNPに属する場合は，古典計算機でその正しさを検証することができるが， NPに属さない問題を解く場合には，この方法が使えないので，量子計算機が正しく実装されているか検証する必要がある． もちろん，個別の回路が正しく実装されれば，計算結果は正しく得られる．個々の回路でのエラーが想定される範囲であれば，誤り訂正によって訂正することは可能である．しかし，エラーに予期せぬ相関が生じ，全体で想定外のエラーが起きる可能性は否定できないので，そのような事態に備えて，本当に回路全体で正しく量子計算機が動作したか検証する必要がある．しかし，計算結果がわからないから計算を行うため，計算結果を以って，計算結果の正しさを検証することは困難である． 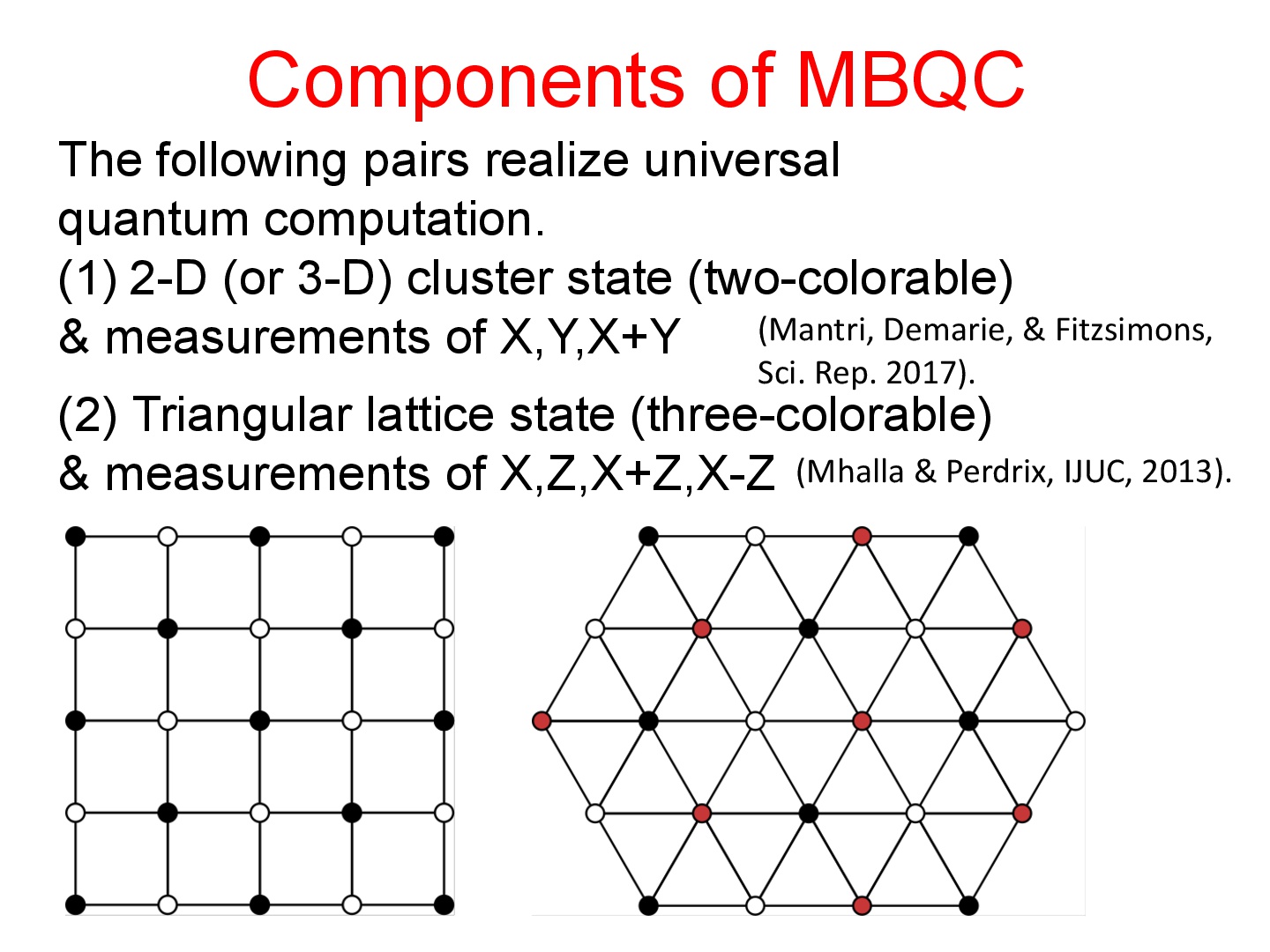本講演では，このような問題を避けるために，測定型量子計算のモデルに注目する．測定型量子計算のモデルでは，全体の形が確定した巨大なエンタングル状態と個別の系の量子測定の組み合わせを用いて計算を行う．個別の量子測定と巨大なエンタングル状態が正しく実装されれば，正しい計算結果が得られるため，これらの構成要素が正しく実装されているか検証することで，測定型量子計算のモデルでの検証が可能となる． 主に以下の３つの設定について議論する． （１）個別の局所測定はノイズなしに実装でき，巨大なエンタングル状態のみ検証が必要な場合． （２）個別の局所測定はノイズがあるものそのノイズは一定の範囲に収まる範囲で実装でき，巨大なエンタングル状態のみ検証が必要な場合． （誤り訂正を組み合わせることで，エンタングル状態および測定の双方に一定の範囲のエラーを許す．） （３）個別の局所測定及び巨大なエンタングル状態の双方を検証する必要な場合． （エンタングル状態および測定の双方に一定の範囲のエラーを許さない．） 近年では，これらの設定において，様々な派生バージョンが議論されており，それらについても紹介する予定である．

第24回講演会（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2018年11月12日(月) 16:00〜17:30
会場：東北大学 情報科学研究棟 大講義室
講演者：李 聖林 (広島大学)
タイトル：反応拡散系で解く生命科学の謎、そして反応拡散形成で導く生命科学の美
概要：近年、実験手法や分子生物学の飛躍的発展により、生命現象における様々な仕組みを細胞や遺伝子レベルまで解析可能となった。それと同時に、実験でみられる結果は局所的な観察に限定されることが多く、それを補うために数理を用いた融合研究が活発になってきている。生命科学における数理の役割は大きく二つあると考えられる。一つは、生物学的新しい現象は既に実験で見られていて、その検証のための定量化や解析に用いられる事、二つ目の役割は、実験では全く予想不可能だった新しい生命の仕組みを発見・提案する事である。本講演では、この１０年間、反応拡散系を用いて明らかにしてきた生命・医療の研究の中から、生命科学における数理の二つ目の役割の事例を重点的に紹介する。また時間があれば、今まで未解決に残っている数学的問題を紹介し、反応拡散系の更なる可能性を探りたい。具体的には、（１）核内クロマチンパターン形成とPhase-field法（２）蕁麻疹の謎を解いた一行の反応拡散方程式（３）非対称細胞分裂における細胞極性と反応拡散系とPhase-field法の３つを中心に紹介したい。

第23回講演会（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2018年10月12日(金) 16:00〜17:30
会場：東北大学 情報科学研究棟 2階中講義室
講演者：Pierre Antoine Geslin (Tohoku University)
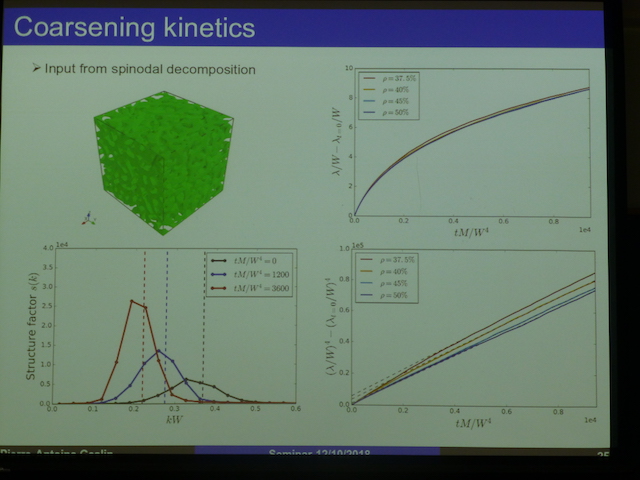
タイトル：Phase-field modeling: application to liquid metal dealloying.
概要：Phase-field modeling has emerged in the field of materials sicence as a tool of choice to investigate a variety of free boundary problems such as alloy solidification, grain growth, brittle fracture or dewetting. This approach consists in introducing a field that defines implicitly the interfaces between the different phases. Partial differential equations on this phase-field and on other relevant parameters are then chosen to incorporate the appropriate physics for the problem at hand. In the first part of my talk, I will present the general framework of phase-field modeling and discuss its capabilities to study various free boundary problems. In the second part of my talk, I will present its application to investigate the formation mechanism of microstructures obtained from liquid metal dealloying. This new processing technique enables to manufacture finely porous structures of various nature (non-noble metals, refractory metals or semi-conductors) presenting a high surface area, valuable in numerous applications (catalysis, battery materials, sensors,...). The development of a phase-field model allowed to clarify the details of the formation mechanism that can be seen as an interfacial spinodal decomposition. In addition, we show that the dealloying process is limited by diffusion of the dealloyed element in the liquid melt and we relate the size of the obtained microstructure to the dealloying rate.

第22回講演会（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2018年10月04日(木) 16:00〜17:30
会場：東北大学 情報科学研究棟 2階大講義室 ６階小講義室(変更)
講演者：中田 芳史 (東京大学)
タイトル：量子情報科学とユニタリ・デザイン
概要：物理法則に支配されたこの世界で実現しうる究極の情報処理とは何だろうか。そんな問いかけに答え、あわよくば実際に実現しようとする学問が、量子論と呼ばれる物理の基本法則と情報科学を融合させた量子情報科学である。量子論においてはしばしば非直感的な現象が起こるが、そのような奇妙な量子現象を情報処理に活用することで、性能が飛躍的に向上する場合がある。量子情報科学では、そういった量子論に基づく情報処理の可能性と限界を見極めるべく、日々、研究を行っている。そんな量子情報科学において、ここ数年、注目を浴びているのがユニタリ・デザインと呼ばれるユニタリ群上での確率分布である。ユニタリ・デザインは、ある意味で量子論における “ランダムな操作”に対応するもので、多くの量子情報処理に役立つ貴重なリソースとなっている。その一方で、ユニタリ・デザインに対応する操作を実験で実現することは容易ではないという欠点も併せ持つため、実験的に易しい手法で実現可能なユニタリ・デザインの構成方法を求めて、多くの研究が行われている。本講演ではまず、量子情報科学の簡単な紹介を行った上で、実験的に簡潔なユニタリ・デザインの構成方法について、近年の研究進展を踏まえつつ詳しく解説する予定である。また、講演者らによって発見された構成方法に関連する組み合わせ論の問題についても紹介したいと考えている。

第21回講演会（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2018年3月12日(月) 16:30〜17:30
会場：東北大学 情報科学研究棟 2階大講義室
講演者：Massimo Lanza de Cristoforis (University of Padova, Italy)
タイトル：A functional analytic approach to singular perturbation problems
概要：The analysis of singular domain perturbation problems for linear equations and systems of partial differential equations has caught the attention of several authors. In particular, a wide literature has been dedicated to the study of boundary value problems defined in domains with small holes or inclusions shrinking to points. This type of problems is of interest not only for the mathematical aspects but also in view of concrete applications to the investigation of physical models in fluid mechanics, in elasticity, and in heat conduction. For example, problems on domains with small holes or inclusions can arise in the modeling of dilute composites or of perforated elastic bodies. Investigating the effect of small perforations in the domains on the solutions of boundary value problems can help us to design objects, with improved characteristics. This is done via the so-called `topological optimization' whose aim is to understand, for example, whether removing  some material can improve the properties of a body. At the same time, knowing the behavior of solutions in domains with cavities can be the starting point of algorithms for the detections of holes and inclusions. However,  the computational analysis of the structures consisting of components with very different lengths or dimensions  often leads to numerical inaccuracy and instability. Therefore, one needs to perform a preliminary theoretical study. The most common approach to analyze problems in a domain with small holes is the one of asymptotic analysis, whose goal is to compute asymptotic expansions in terms of the size of the perforations. In this talk, we present an alternative method, i.e. the Functional Analytic Approach. Such a method aims at representing the solution or related functionals in terms of analytic maps and explicitly known functions. As a consequence one can express the solutions in terms of power series of the perturbation parameter whose coefficients can be explicitly computed. The method has revealed to be extremely versatile, with applications to several geometric settings and also to nonlinear boundary conditions.

第20回講演会（知の創出センター共催）（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2018年2月15日(木) 16:30〜17:30
会場：東北大学知の館(TOKYO ELECTRON House of Creativity) 3階
講演者：浦本 武雄 (東北大学大学院 情報科学研究科)
タイトル：計算階層の分類と、その圏論的見方
概要：例えば11010の様なバイナリ列が与えられ、それを２進数と見たときに、それが合成数か 否かを判定するアルゴリズムは勿論ありますが、そのアルゴリズムはどの程度まで効率化 することができるでしょうか？あるいは原理的にこれ以上効率化できないという限界を見 極めるにはどうすれば良いでしょうか？———この種の、文字列を入力として受け取り一 定の性質を判定する問題及びその計算量を見積もる問題は多くの文脈で自然に現れる問題 ですが、形式的には文字列の集合(言語)の組合せ論的な問題として定式化されます。形式言 語理論と呼ばれる分野では古くから、この様な組合せ論的な問題に対する研究が行われて きましたが、近年、あるクラスの言語に対する見通しの良い分類理論が整備され研究が進 んでいます。本講演では、文字列に対する判定アルゴリズムの話から始め、その問題のク ラスの良い分類を目指す過程で、いかにして数学の一分野である「圏論」が使われるのか について、自身の研究を踏まえてお話しします。

第19回講演会（数理科学連携研究センター共催）（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2018年1月10日(水) 15:00〜16:00
会場：東北大学 情報科学研究科 大講義室
講演者：Braxton Osting (The University of Utah, USA)
タイトル：Geometric and variational methods for clustering
概要：Clustering is the unsupervised learning task of finding similar groups of items within a dataset. One approach to clustering is to reformulate the problem as a weighted graph partitioning problem where the graph edge weights are derived from a similarity measure between items in the dataset. This graph partitioning problem can be formulated using a variety of geometric quantities, for example, the Cheeger cut and Laplace-Dirichlet eigenvalues. In this talk, I’ll discuss the resulting methods, their semi-supervised extensions, variational relaxations, and interpretations in terms of random processes. I’ll present some recent consistency results for geometric graphs, stating convergence of graph partitions to an appropriate continuum partition. I’ll also describe numerical methods that can be used to find locally optimal partitions and present results demonstrating that such methods compare well with state-of-the-art approaches on a variety of graphs constructed from synthetic data, the MNIST handwritten digit dataset, and images. This general-audience colloquium will be complemented by three more mathematical lectures on the same topic.

第18回講演会（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2017年10月31日（火）16:00〜17:20
会場：東北大学　情報科学研究科棟　中講義室
講演者：Sergey Minaev (Far-Eastern Federal University, Russia)
タイトル：Hierarchy of nonlinear equations of combustion theory
概要：In mathematical modeling of combustion processes there is a wide range of different problems related to fluid mechanics, gas dynamics, chemical kinetics and nonlinear physics. An analytical study within the framework of complete models that take into account all the characteristics of combustion is practically impossible because of the large span in time and spatial scale of the processes. In this case, the only realistic approach is the use of simplified nonlinear equations aimed at describing a specific phenomenon. The seminar will discuss simplified nonlinear models of flame front instability and their exact solutions, nonlinear models arising in the chemical kinetics of combustion and models describing localized in the space individual hot spots of combustion. The discussion will be attended by Dr. Viatcheslav Bykov (Karslruhe Institute of Technology , Germany), specialist in reduction of chemical kinetics model and Dr. Vladimir Gubernov (P.N. Lebedev Physical Institute of the Russian Academy of Sciences, Moscow, Russia), specialist in nonlinear dynamics of reactive-diffusion systems.

第17回講演会（終了しました）（第3回人工知能学研究会の一部としての開催です）

（ポスター（PDF ファイル）はこちら）

日程：2017年10月11日（水）15:10〜16:00
会場：東北大学　情報科学研究科棟　大講義室
講演者：石川 博 (早稲田大学 理工学術院)
タイトル：視覚の数理モデルと構造付き予測問題
概要：視覚は人間の感覚入力のうちおそらく最も大量の情報を処理するものだが、 それでも周りの環境についての情報のうち、ごく一部を２次元の画像として得 て、そこから脳内で最も可能性の高い情景を再構築しているものである。そ のためには、ありうる情景の情報表現があらかじめ存在している必要である が、コンピューター上の画像や、網膜上に並ぶ視細胞の信号の総体としての 視覚入力の表現は、一般性が高い一方、見えている物体や状況の認識につ なげるための構造を明示的に表現しない。しかし記憶容量、効率、そして汎 化性の観点からは、まさにそのような偶然でない構造を情報表現することが 必要である。最近の人工知能ブームの原因である畳み込みニューラルネット ワークは、その構造から暗黙のうちにそのような表現をしていると思われる。 本講演ではこれらの点を説明した後、JST CREST 数理モデリング領域にお けるプロジェクトで進めている研究のうち、構造付き予測問題の最新成果（ラ フ画の線画化、白黒写真のカラー化、画像補間）を紹介する。

第16回講演会（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2017年6月29日（木）16：30～17：30
会場：東北大学　情報科学研究科棟　大講義室
講演者：飯田 渓太（東北大学 東北メディカル・メガバンク機構、大学院医学系研究科）
タイトル：遺伝子発現系の数理モデリング〜確率論と決定論の視点から〜
概要：遺伝子発現とはDNA情報からタンパク質が合成される過程である。この原理は1950年代 に提唱されたが、一方でその発現量に関しては法則性が確立していない。定量的な遺伝 子発現解析は従来さまざまなアプローチが試みられているが、未だに決定的な方法が見 つかっていない。一方、21世紀のシステム生物学は複雑な細胞内分子ネットワークの構 造を明らかにしてきたが、遺伝子発現ネットワーク上のダイナミクスについては、ゆらぎを 「平均化」して無視するという単純化がしばしば行われており、その解釈については疑問 が残っている。この問題に対し、タンパク質の生成崩壊の過程をMarkovモデルを用いて表 し、確率分布をマスター方程式から計算する方法が提唱されているが、一般にマスター方 程式は解析が難しく、非常に単純なモデルであっても解析解が求まらない場合が多い（転 写、翻訳のtwo-stage modelなど）。 今回は、遺伝子発現ネットワークのモジュールとなる基本数理モデルを新規に提案し、そ の解析解を導出する。また、我々の提唱するモデル方程式が１細胞からN細胞の平均化 モデルまで広範囲に適用できることを示す。さらに、この１細胞モデルと平均化モデルは 本質的に異なるものであることを明らかにし、実験で得られる発現量のアンサンブル平均 に決定論的モデルを当てはめることの危険性を示唆する。

第15回講演会（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2017年6月15日（木）16：30～17：30
会場：東北大学　情報科学研究科棟　大講義室
講演者：水藤 寛（東北大学 材料科学高等研究所）
タイトル：臨床医学と数理科学の協働の現状と可能性
概要：本講演では、科学技術振興機構の戦略的創造研究推進事業CRESTにお けるプロジェクト「臨床医療における数理モデリングの新たな展開」で進め ている内容を中心に、主に大動脈における血流解析の話題について述べ る。大動脈における血流は、動脈硬化から始まって大動脈瘤、大動脈解 離など生命に関わる循環器系疾患に深く関係していると考えられており、 曲率を持つ管内の流れに特徴的な2次流れや捩率の影響、拍動流である ことによる特徴、血管壁との流体構造連成など、様々な流体力学的特徴 を持っている。血管形状には個人差が大きく、それらの幾何学的な特徴と 病態との関係を調べることによって予後予測にもつながることが期待され ている。また、このような解析にはCT, MRIなどの医用画像を用いることに なるが、その処理においても数学的手法が重要な役割を果たしている。本 講演では、このような数理科学と臨床医学との協働の営みを紹介し、その 可能性について述べたい。

第14回講演会（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2017年6月1日（木）16：30～17：30
会場：東北大学　情報科学研究科棟　大講義室
講演者：水木 敬明（東北大学 サイバーサイエンスセンター）
タイトル：秘密計算を実現するカードベース暗号
概要：仲良しグループが今度の土曜日にカラオケに行くかどうかを決めたい場面を考え る。気まずくなるのを避けるため、各人の行きたいかどうかの気持ち（YES/NO） は秘密にしたまま、全員がYESであるか、それとも一人でもNOの人がいるのか、 そのどちらであるかだけを知りたい。すなわち、全員の秘密のビット値の論理積 （AND演算）の結果だけを知りたい。もしこのような「秘密計算」が可能であれば、 前者の場合はもちろんカラオケに行くことにし、後者の場合は今回はやめておくこ とができる（後者のときも、誰がNOと思っているかわからないので、気まずくなら ない）。 本講演では、トランプのような物理的なカード組を使う「カードベース暗号」を用い ると、上述のような秘密計算が簡単に実現できることを紹介する。特に、講演者ら が考案した「ランダム二等分割カット」というシャッフルの登場により、論理積や排 他的論理和（XOR）の秘密計算が少ないカード枚数や手順で実行できるようにな り、カードベース暗号が急激に効率化され、人間が実際に実行できるレベルに なっていることなどを含め、カードベース暗号の歴史と最近の動向を概観する。

第13回講演会（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2017年3月28日（火）16：30～17：30
会場：東北大学　情報科学研究科棟　大講義室
講演者：Riccardo Adami（Politecnico di Torino, Italy）
タイトル：The critical occurrence of negative energy ground states for a critical non-linear Schroedinger equation
概要：It is well known that the nonlinear Schrodinger equation models the light wave propagation in optical fibers. The study of wave propagation in variously shaped devices, such as Y-junctions, H-junctions has gained its popularity in recent years. To understand the properties of the propagation, a key role is played by the behaviour of a special solution minimizing the energy, called ground state. For the so-called "L^2 critical" Nonlinear Schrodinger equation considered on the Euclid space, ground states cannot have negative energy: indeed, for a ground state to exist it is necessary that the nonlinearity is focusing, and the computation of the moment of inerzia due to Glassey shows that every state with negative energy blows up. We show that if the spatial domain is a quantum graph, then the compact core of the graph can trap negative energy ground states if some topological assumption is satisfied. This is a joint result with Enrico Serra e Paolo Tilli.

第12回講演会（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2017年3月7日（火）16：30～17：30
会場：東北大学　情報科学研究科棟　大講義室
講演者：富安亮子(山形大学理学部/ JST さきがけ)
タイトル：格子とその結晶学への応用
概要：結晶学は固体物質のミクロ構造の情報をどのように得て処理するかという観測の問題を 扱う分野で、実験物理と、各実験装置に付属するデータ解析(最適化、ときに第一原理 計算まで含む)ソフトウェアアプリケーションがその基盤を支えている。数学上の意味で 困難な問題も存在することから、計算面において様々なアプローチがこれまでになされ てきたが、情報科学分野との連携はまだ発展途上と言える。数学分野との連携について は、およそ100年前に結晶学が創始されて以来、格子パラメータを記述するために格子 基底簡約理論が、消滅則を記述するために結晶群に関わる群論が導入されたなど数多 くの事例があり、この他の事例については割愛するが、結晶群の記法において、一つの 空間群に対して複数の記号が対応してしまうという問題を解決するため、新しい記法が Conway, Thurstonらによって提案されたのは近年のことである。この事例が示すように、 この分野では解析・ソフトウェアアプリケーションにおける障害として、数学としては基本 的な(でも新しい)問題が残っていることがある。 今回は主に消滅則の話である。230通りの空間群に対して、およそ1700通りの消滅則が 発生するが、コードを書く際にそんなにたくさんの場合分けはできないので「この消滅則 に共通する性質は何か?」という問題が発生する。消滅則は、数学的に言えば、multiple invariant theoryの問題とも言えるが、この分野を牽引したHilbertの第14問題と、必要とさ れている「性質」の間の距離は遠く、そこで、異なるタイプの「定理」を計算によって見つけ てきた、というのが、得られた結果の趣旨である。この話が、整数論の結果とも絡めて 「格子ベクトル長さの情報から格子を決定する(粉末指数付け)」という問題に応用される。 定理自体は、電子顕微鏡など、消滅則に関わる一般的な問題に使用することができる。

第11回講演会（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2017年3月6日（月）15：30～16：30
会場：東北大学　情報科学研究科棟　中講義室
講演者：林 直樹 (大阪大学大学院工学研究科)
タイトル：代数的グラフ理論に基づく マルチエージェントシステムの制御と分散最適化
概要：情報通信技術の進展により、ネットワークを介してサブシステムが有機的に結 合した大規模システムを分散的に制御する手法の重要性が増している。このよ うなネットワーク化されたシステムをうまく制御するためには、サブシステム間の 相互作用を考慮した数理的アプローチが必要である。近年、制御工学の分野 では、このようなネットワーク化されたシステムの分散制御法として、代数的グ ラフ理論に基づくマルチエージェントシステムの制御が注目され、ビークル群の 編隊形成や動物の群れ行動の解析、センサネットワーク、スマートグリッドへの 応用などに関する研究が活発にされている。マルチエージェントシステムの最も 基本的な制御法として、合意制御が挙げられる。合意制御とは、エージェント間 の情報伝達を通して全てのエージェントの状態をある値(合意値)に漸近的に 一致させる制御法であり、ネットワークの構造と合意値や収束速度との間には 密接な関係があることが知られている。本講演では、代数的グラフ理論の観点 から、マルチエージェントシステムの合意制御やその分散最適化への応用につ いて紹介する。

第10回講演会（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2017年3月6日（月）14：20～15：20
会場：東北大学　情報科学研究科棟　中講義室
講演者：木村 元 (芝浦工業大学システム理工学部)
タイトル：一般確率論上の情報理論について
概要： 一般確率論(General Probabilistic Theories)とは,古典確率や量子論を 包含する操作主義的に最も一般的な確率論の枠組みである .von Neumannの量子論の数学的特徴付けに端を発し,1960年代からMackey やArakiらによって整備され発展したものである.他方,近年の量子情報 科学の発展に呼応するように,一般確率論を土台とする情報理論を構築 する試みが世界的にすすめられている.これは,古典情報理論及び量子 情報理論を含む「操作主義的に最も一般的な情報理論」であると考えられ, この研究により情報処理や物理法則の間の連関性を理解し,情報の本質 を捉えることができると期待されている. 本講演では,一般確率論の簡単なレビューに加え,情報理論の基礎概念 であるエントロピーの導入や,通信や暗号理論の基礎となる「情報取得量 の限界」や「情報源符号化定理」に関し,最近の我々の成果について紹介 する.

第９回講演会（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2017年2月24日（金）16：30～17：30
会場：東北大学　情報科学研究科棟　大講義室
講演者：佐野 吉彦（静岡大学 工学部）
タイトル：局所体積平均理論に基づく多孔質機器の設計
概要：従来、微細な構造体が複数集まった多孔質体の工業製品は、 熱交換器・触媒・燃料電池など工学・産業界等で幅広く活用されて きた。このような多孔質体の特徴は、一般的に機器サイズ（マクロ スケール）と構造物サイズ（ミクロスケール）に大きな隔たりがある ことである。更に、微細構造が周期性を有するときもあれば、ランダム な配置のときもあり、その形状や配列により機器の性能は大きく左右 される。機器の開発現場では，主に数値シミュレーションに基づき 機器の最適設計を行うが、その際、両スケールの物理現象を連成 させる必要があり、実用性の高い連成手法が要求されている。 本講演では、マルチスケール・マルチフィジクス現象を記述 するために、工学で発展した局所体積平均理論を紹介する。 講演者の研究テーマから、熱・物質移動現象を例に、ミクロ とマクロの物理現象について説明していく。

第８回講演会（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2017年2月23日（木）15：10～16：10
会場：東北大学　情報科学研究科棟　大講義室
講演者：井上 歩（愛知教育大学 数学教育講座）
タイトル：対象を代数化することで見えてくる世界 （紐の絡まりを表現する方法）
概要： 近年、高分子といった複雑な構造を代数化して、その構造や 性質を解析するという手法（パーシステントホモロジー）が 脚光を浴びている。このように対象を代数的に表して解析する ことは、今後の科学の発展にも重要な手法と言える。そこで 本講演では、紐の絡まりを対象として、これがカンドルという 代数で表現できることを紹介する。紐状の物質の絡まりは DNA やタンパク質構造といった形で自然界に遍在しており、この 代数化はこれらの研究にも応用が期待できる。例えば、 絡まった紐をカンドルとして表すことで、そのキラル性を簡潔に 表現することができる。また本講演では、絡まった紐から どのような思考を経てカンドルという代数を想起するのか、 その仕組みについても解説する。

第７回講演会（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2017年2月16日（木）16:30～17:30
会場：東北大学　情報科学研究科棟　大講義室
講演者：横山 啓一（日本原子力研究開発機構）
タイトル：量子ウォークを用いた同位体分離スキームと 放射性廃棄物無害化技術への応用
概要：原発から発生した放射性廃棄物の無害化を目指して、 中性子照射による長寿命核種の核変換が検討され ている。しかし、核種によっては今までにない精密な 同位体分離が必要となるため、効率の良い分離原理 が望まれている。 我々は、分子集団の回転状態分布に着目した時、あ る種の光吸収により回転角運動量空間で量子拡散 が実装されることを見出した。量子ウォークが持つ線 形拡散と局在化の性質により、従来より遥かに精密 な同位体分離を実現できる可能性が出てきた。講演 では今後の課題と発展性についても紹介したい。

第６回講演会（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2017年2月8日（水）16：30～17：30
会場：東北大学　情報科学研究科棟　中講義室
講演者：鈴木 厚（大阪大学サイバーメディアセンター）
タイトル：大規模疎行列の並列直接法解法とFreeFem++ソフトウェアでの活用
概要：偏微分方程式を有限要素法で離散化すると、大規模な疎行列からなる連立方程式系が 得られる。その解法にはLU分解に代表される直接法と共役勾配法に代表される反復法 がある。反復法は計算複雑さが小さく、主たる演算である行列とベクトルの積演算が並列 計算に適するが、非対称性が強い場合や不定値の場合には適切な前処理と組み合わせ る必要がある。一方直接法は堅牢な解法であるが逐次演算であること、計算複雑さが大 きいため、大規模行列を扱うことは難しかった。しかし、 変数の順序の並べ替えと非零成 分のグラフ分割により、複数の箇所から分解を開始することと部分的な密行列演算操作 の抽出により、現代のスーパースカラー型のマルチコアCPUシステムで高い演算性能を得 ることが可能になってきている。数学的な問題は、有限要素法剛性行列は対称な非零要 素パターンを持つため、行列の左右から同一の置換をほどこす対称軸選択が効率的であ るが、不定値行列の場合はLU分解が途中で破綻する可能性があることである。分解途中 の部分行列の対角成分が極端に小さくなった場合、LU分解操作を先送りすること、対角 を2x2のブロックとして扱うことでこの問題を回避することができる。開発した Dissection コードは更に行列が特異な場合、核の次元を数値的に決定するアルゴリズムを含む。 FreeFem++ は有限要素法の弱形式を直接記述するスクリプト言語を持つ汎用プログラム であり、三角形あるいは四面体要素分割の上での種々の有限要素空間を設定し、剛性 行列を生成できる。不定値行列を導く混合型有限要素法の代表例である、非圧縮流れ問 題、静磁場問題、半導体問題でのDissectionコードの有効性を示す。二次元問題では、 スーパースカラーCPUに最適化した直接法は反復法より高速であり、100万自由度を超え る大規模な3次元問題では、領域分割と組み合わせ効率的な前処理を構成することがで きる。

第５回講演会（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2017年2月8日（水）15：20～16：20
会場：東北大学　情報科学研究科棟　中講義室
講演者：大塚 厚二（広島国際学院大学）
タイトル：Programming by FreeFem++ and its application to shape optimization
概要：数理モデルの研究では数学的妥当性の下で、モデリング・連続体定式化・ 離散化・数値計算・可視化といった一連の流れが必要となる。一連の流れを シームレスに扱うツールが欲しくなり、1994 年ごろにパリ第６大学のO. Pironneau教授とF. Hecht教授によるFreeFEMプロジェクトを知った。シーム レスに扱う方法は数理研究者に役立つと考えて「有限要素法で学ぶ現象と 数理」を著した。第１章が連続体定式化、第２・３章が単独方程式の離散化・ 数値計算・可視化、第４章で連続体、第５章では反応拡散に応用し、最後が 数学理論との対応になっている。講演では、第４章２節の固体力学までにつ いてFreeFem++を使う研究方法をサンプルで示し、最後に、筆者の研究テー マである「偏微分方程式境界値問題における特異点集合の形状最適化」へ の応用について紹介する。本を持たない聴衆のため、下記サイトに資料を 用意しておく。 http://www.comfos.org/jp/ffempp/book/course

第４回講演会（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2017年1月27日（金）16：30～17：30
会場：東北大学　情報科学研究科棟　大講義室
講演者：藤原 祐一郎（千葉大学大学院融合科学研究科）
タイトル：Reverse-complement対応型difference systems of setsとそのDNAストレージへの応用
概要： 有限巡回群の部分集合族のうち，ある種の組合せ的条件を満たすものとして， difference systems of sets (DDS) というものがある．DSSは本来，情報通信に おける同期問題を解決するための組合せ構造として提案されたが，以後，純粋に 組合せ論の観点からも，その存在性などが研究されてきた． 本講演では，reverse-complement DSSという，DNAに情報を記録する仕組みに有用な DSSの変種を提案し，その組合せ論的構成法などを紹介する．

第３回講演会（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2017年1月11日（水）16：30～17：30
会場：東北大学　情報科学研究科棟　大講義室
講演者：坂上 貴之（京都大学大学院理学研究科・教授）
タイトル：応用複素関数論による流体数理コンセプトモデルと諸分野連携
概要： 二次元非粘性・非圧縮流体が正則関数と等価であ ることは，はるか100年以上も前から知られた古典的事実 であり，当時の翼理論などに代表される工学的な諸問題 の多くは複素関数論を通して本質的な理解が進められて きた．京コンピュータに代表される大規模数値計算が利 用可能な現代にあって，こうしたいわゆる「素朴すぎる」 とも言える数理モデルにはもはや解決できるような課題 はないのだろうか？確かに工学的に流体運動を記述する 偏微分方程式などが明確な問題であれば，それを数値計 算で解けば定量的な近似値は得られるが，我々はその対 象となる問題がこれまでに扱われなかった，例えば環境 や生命現象に関わるものであるような場合，依然として 定性的側面や本質的なメカニズムの理解においてこうし た素朴な流体モデルは我々に教えてくれることは多い． 同時に，こうした古典的な重要性に鑑みて100年以上前に スタートした複素関数論の応用数学研究が長い時を経て 他の数学分野の発展や計算機などとのつながりを得て日 々進歩し，現在，新しい応用研究の萌芽として再発見さ れつつある．本講演では，講演者がJST さきがけやCREST から始まり現在に続く一連の研究を紹介し，数学と諸分 野について，数学者の立場としての連携のあり方，また これらのモチベーションが新しい数学としての研究対象 を生み出す協調関係につながるかどうかの可能性などに ついて，参加者の皆さんと議論できればと考えている．

第２回講演会（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2016年12月22日（木）16：30～17：30
会場：東北大学　情報科学研究科棟　中講義室
講演者：丸橋弘治（株式会社富士通研究所・知識情報処理研究所・人工知能研究センター・シニアリサーチャー）
タイトル：テンソル分解を用いた大規模実データ分析
概要： ネットワーク通信ログやＷｅｂアクセスログ、ＰＯＳデータといった、人や機器などの要素間関係を記録したデータから、 不正行為などを発見することが、セキュリティやマーケティングなどの分野で求められている。本講演では、要素間関係を 表すデータをテンソルとみなし、テンソル分解を用いて要素間関係の分布をモデル化することにより、特徴的な要素間関係 を検知する、いくつかの事例を紹介する。また、近年注目を浴びているDeep Learningを応用した、要素間関係分析の試みも紹介する。

第１回講演会（終了しました）

（ポスター（PDF ファイル）はこちら）

日程：2016年12月8日（木）16:30～17:30
会場：東北大学　情報科学研究科棟　大講義室
講演者：池村淑道（長浜バイオ大学客員・名誉教授、国立遺伝学研究所・総合研究大学院大学名誉教授）
タイトル：ゲノムビッグデータからの教師なし学習による想定外知識発見と社会的重要課題への応用
概要：ゲノム配列を代表例とする、生命科学分野の多様な測定データはビッグデータ化しており、そこにどの様な興味深い新知識が潜んでいるのかは想像することすら困難と思える。 この様な状況下では、モデルや仮説や予備知識なしにビッグデータを研究できる「教師なし機械学習」が威力を発揮する。ゲノム配列はATGCの4種類の文字で構成される長文と言える が、その文章中の連続文字列（例えば５連や６連、あるいは20連続文字）についての「ワードカウントに着目した機械学習」を行ってきた。ワードカウントのような理解しやすい解析 を行うことでも、想定外の多様な知識発見が可能になる。20連文字を対象にした場合、約一兆一千億（$=4^{20}$） 次元のデータ解析となり、スパースな大量データ解析となる。「コンピュータでエボラやインフルエンザウイルスの弱みを探る」 等の社会的に重要な課題への応用も可能になっている。