注意 以下のメールアドレスの後に tohoku.ac.jp をつけて下さい。
(A01-2) 鮑研究室の研究分野は低次元位相幾何学です。主に３次元空間にある曲線（結び目）とグラフ（空間グラフ）、そして３次元多様体を研究対象としています。
２次元平面上の単純閉曲線は、ジョルダン・シェーンフリースの定理により、必ず円板を張ります。３次元空間にある単純閉曲線なら、円板を張らないものもたくさんあります。次の図(a)(b)は円板を張る閉曲線の例で、(c)(d)は円板を張らない閉曲線の例です。よって、３次元空間にある曲線の“形相”を調べることは興味深い課題になります。
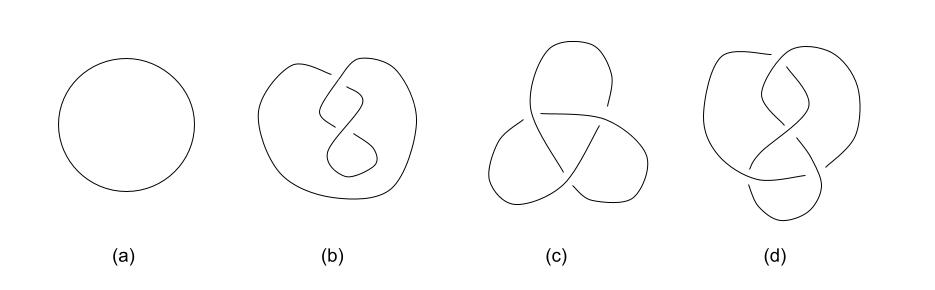
上のような閉曲線のことを位相幾何学では結び目と呼びます。線を切ることなく一方から他方へ変形できる時、本質的に同じ結び目（同値な結び目）と考えます。円板を張る結び目は図(a)の円周と同値です。図(c)と(d)は両方とも円板を張らないが、同値な結び目ではありません。結び目理論では、この考え方のもとで、結び目の同値性や位相的な性質を様々な手法を用いて研究しています。以下、結び目を研究する方法をいくつか紹介します。
多様体の基本群やホモロジー群を使って結び目を研究することができます。３次元空間から結び目の開近傍を除くと結び目補空間という境界付き３次元多様体を得ることができます。結び目補空間の基本群から結び目に関する様々な情報が得られます。例えば、Alexander 多項式という古典的不変量は基本群の群表示から計算できます。
上のような古典的な手法以外、Jones 多項式をはじめとして数多くの新しい結び目不変量が1980代以降発見されました。それらの不変量は現在量子不変量と呼ばれ、量子群とその表現を用いて構成することができます。この構成法がとても強力で、古典的不変量である Alexander 多項式も量子不変量として再構成することができます。
2000年前後、Ozsváth と Szabó は Lagrangian Floer ホモロジーを利用して、Heegaard Floer ホモロジーと呼ばれる3次元多様体及び結び目の不変量を作りました。この不変量の位相的な応用として、結び目同境群、結び目解消数、結び目の手術などについての研究がたくさんあります。現在、このホモロジーの量子不変量との関係について注目され、多くの研究結果が出ています。
代数や解析など、数学の多くの考え方は結び目の研究に生かされているのが現代結び目理論の特徴だと思います。
一次元単体複体（グラフ）の３次元空間への埋め込みを空間グラフと呼びます。空間グラフは結び目の拡張として重要な研究対象であり、高分子化合物の数学的モデルとしても注目されつつあります。結び目に関する理論があれば、この理論を空間グラフまで拡張できるかどうかが自然な疑問です。例えば、量子不変量は結び目からグラフへの拡張が基本的に可能です。一方で、結び目解消数や結び目のザイフェルト曲面など、空間グラフへうまく拡張できない概念もたくさんあります。
局所的に３次元空間と同相であるような可算基底を持つ Hausdorff 位相空間を３次元多様体と言います。結び目から３次元多様体を構成する方法がいくつか挙げられます。先ほど述べた結び目補空間以外、分岐被覆と Dehn 手術を用いて考える方法があります。任意の向き付けられた閉３次元多様体は、３次元球面の結び目での分岐被覆として実現されます（Alexander の定理）。そして、任意の向き付けられた閉３次元多様体は絡み目に沿った手術で得られます（Kirby Calculus）。このような関係のもとで、結び目の研究と３次元多様体の研究は、相互に影響を与え合います。
当研究室の研究分野に興味があれば、どうぞお気軽にメールでお問い合わせください。
次の二冊は結び目とはどういうものかをわかりやすく説明してくれた本です。高校生向けですので、予備知識がなくても読めます。練習問題を解いてみって面白いと感じるかどうか、試してみてください。
(1) 村上斉, 結び目のはなし, 日本評論社
(2) Colin Conrad Adams, The Knot Book, W.H. Freeman and Company, New York, 1994.
次の三冊は結び目理論を勉強したい学部四年生また修士一年生におすすめの本です。
(3) W.B.R. Lickorish, An Introduction to Knot Theory, GTM 175, Springer-Verlag, New York, 1997.
(4) Dale Rolfsen, Knots and links, Corrected reprint of the 1976 original, Mathematics Lecture Series, 7, Publish or Perish, Inc., Houston, TX, 1990.
(5) 村上斉, 結び目理論入門（上）, 岩波書店
次は結び目の量子不変量について知りたい方におすすめの入門書です。
(6) 村上順, 結び目と量子群（すうがくの風景）, 朝倉書店
(A02-1) 須川研究室では複素１変数函数論を中心に、リーマン面、タイヒミュラー空間、クライン群、擬等角写像、Loewner方程式、複素力学系・フラクタルなどの周辺分野を研究していますが、特に以下の対象に興味を持っています。
解析函数（特に等角写像）の性質を幾何的に研究したり、逆に解析函数の持つ深い性質を利用してリーマン面の幾何学を研究したりしています。等角写像は流体力学や電磁気学などにも応用を持っています。
リーマン面の複素構造の変形を考える際に今や必要不可欠となった概念です。特に解析函数が全平面の擬等角写像に拡張できるための条件や、退化ベルトラミ方程式についても研究を行っています。退化ベルトラミ方程式は超音速での気体の流れの解析に応用があります。また、擬等角写像は最近の脳科学にも応用されつつあります。
楕円函数・特殊函数を含む古典理論から、複素力学系、微分従属式、タイヒミュラー理論、シュワルツ微分などをキーワードとする現代理論まで広くカバーしています。
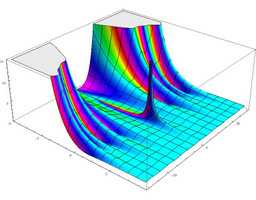
[リーマンゼータ函数の表現例：高さは絶対値、色相は偏角を表す。]
複素解析学をさらに深く勉強したい人は言うに及ばず、コンピュータ実験によって何か面白い数学的現象を観察したい人、新しい公式を発見したい人、とにかく計算が好きな人など、個性的な学生を歓迎します。また、社会人・留学生も積極的に受け入れます。
(A02-2) 松原＝許研究室では、主に特殊関数論や代数解析学の立場から、微分方程式の研究に取り組んでいる。中でも、超幾何関数と呼ばれる、様々な数学の場面で顔を出す“普遍的な特殊関数”が研究の中心である。最近では、代数統計学や場の量子論といった、数学だけでなく他の分野に由来する研究テーマや研究手法にも挑戦している。周期積分、代数的 de Rham コホモロジー群、交叉理論、D加群、多変数判別式、凸多面体の組み合わせ論など、一見難しそうな言葉が並ぶが、これらはすべて微分方程式論という大きなテーマの下で結びつき、新たな発見を生み出すための重要な道具となっている。
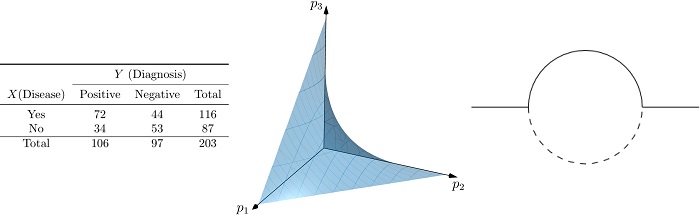
[一見異なる分野にも，超幾何函数は普遍的に現れる．図は全て Gauss の超幾何函数を表す．
左が統計，右は物理，中央はこれらを幾何学的にとらえたもの（Segre 曲面）．]
田中 太初 (Tanaka, Hajime)
教授
htanaka@
本研究室では、代数的グラフ理論、及び関連した組合せ論や離散数学を研究対象としています。
有限グラフにはいくつかの方法で実対称行列を対応させることができ、これらの行列の性質、特に固有値や固有ベクトルの観点からグラフの構造を調べるのが代数的グラフ理論です。学部時代に学んだ線形代数学の知識を深める上で恰好のトピックだと言えます。一方、代数的グラフ理論と相性の良い、正則性の高いグラフ (強正則グラフ・距離正則グラフ・association schemes 等) の具体例には有限群の作用等を用いて代数的に定義されるものが多くあります。このため、代数学 (群論・環論・体論)、特に有限体についていくらか学んでおくと、大きなアドバンテージになるでしょう。
代数的グラフ理論と密接に関わっているテーマとして、グラフ上のランダムウォークや、その量子力学版である量子ウォークがあります。特に後者は21世紀に入って爆発的に発展している分野で、本研究室でも近年精力的に研究しています。また、グラフに付随する行列を確率変数とみなすことにより、量子確率論 (非可換確率論) との関連も生じます。この立場から、グラフの族に対して(量子)中心極限定理等の類似物を考えることも興味深いテーマです。
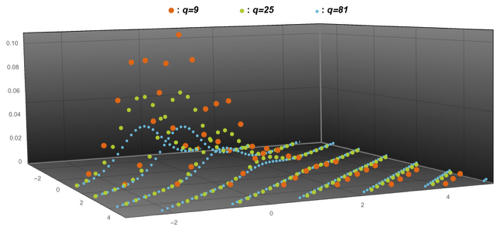
[Paley グラフ $\mathrm{Paley}(q)$ とその補グラフの冪の正規化した同時スペクトル分布]
符号やデザイン等を含む種々の離散数学的対象は、適当なグラフ (association schemes) の頂点集合の部分集合とみなすことができ、この観点からこれらの対象を研究します。符号の場合であれば、例えば「長さ $n$ かつ最小距離が $d$ 以上の$2$元符号の最大サイズ」を考えます。このような研究の潮流は1973年の Delsarte の学位論文に端を発するもので、代数的グラフ理論に加えて線形計画法等の最適化の手法を駆使します。近年は有限幾何や極値集合論の研究にも活用されています。
本研究室を志望される方は、何はともあれ線形代数学をしっかり学んでおいて下さい。特に、「実対称行列の対角化」は代数的グラフ理論の全ての基礎になります。上で述べたトピックについて、いくつか参考文献を挙げます：
なお、「代数的でない一般のグラフ理論を学びたい」或いは「代数学の基礎をしっかり勉強したい」といったご相談にも乗りますので、お気軽にメールでお問い合わせ下さい。
宮島 信也 (Miyajima, Shinya)
教授
miyajima@
本研究室では、数値計算結果が何桁正しいのかを調べる研究をしています。
理工学においては、現象を理解するために数理モデルが作られ、これらのモデルを解くことによって、未知の現象の予測や新たな工学的製品の設計等が可能となります。これらのモデルは解析的な手法で解くことが困難であるため、計算機を用いた数値計算により解かれることがほとんどです。
計算機を用いた数値計算では、その計算は正確には行われません。四則演算の結果はその都度有限桁に近似され、極限を含む無限演算は全て有限演算に近似されます。計算結果から正しい結論を得るためには、計算結果の誤差評価を行って「何桁正しいのか」を確定する必要があります。計算結果のみならず、この「何桁正しいのか」という情報も与える手法を作っています。
(B01-1) 原田研究室では、組合せ論的符号理論と組合せデザイン理論やこれらに関係する組合せ構造やそれらの応用についての研究をしています。
符号理論は、誤りが発生する通信路において、いかに効率よくかつ信頼性が高い情報伝達を行うことが出来るかを研究する分野で、数学、情報科学、実用化技術と、様々な立場での研究が広く行なわれています。
組合せ論的符号理論は、通信路の数理モデルにおいて符号化の部分に現れる組合せ構造としての誤り訂正符号（error-correcting code）を組合せ論な手法で研究を行う符号理論です。本研究室では、主に、有限体上の線形空間において色々な意味での“良い”部分空間の構造の研究を、組合せ論的な手法にて行っています。しばしば計算機による計算も重要な役割を果たします。自己双対符号（self-dual code）と線形補符号（linear complementary code）の２つのクラスを主な研究対象としています。
符号が情報通信を起源にもつ組合せ構造であったように、様々な分野において組合せ論や離散数学は色々な形でその有用性を提示してきていると思われます。組合せデザインもその一つであり、実験計画を起源にもつ組合せ構造です。組合せデザインの研究での基本的な問題を一言で説明すると、全体をよく近似する“良い”部分集合を見つけることであり、本研究室では、良い組合せデザインの構成や符号など他の組合せ構造との関連を意識した組合せデザインの研究を組合せ論的手法で行っています。組合せデザインの研究においても、理論の構築とともに計算機による計算もしばしば重要な役割を果たします。 対称デザイン（symmetric design）とアダマール行列（Hadamard matrix）の２つのクラスを主な研究対象としています。
符号理論や組合せデザイン理論は、理学部・教育学部の数学系の学科などで学んでいる学生さんには馴染みが薄い分野かもしれません。大学院で新たに、情報通信に現れる組合せ構造である誤り訂正符号や実験計画を起源とする組合せ構造である組合せデザインの数学的（組合せ論的）な研究をやりたい学生さんを歓迎します。工学部の情報系の学科で学んでいる学生さんには符号理論は馴染みがある分野だと思います。数学的（組合せ論的）な立場で符号理論の研究をやりたい学生さんを歓迎します。
本研究室に進学を希望する学生さんは、まずは線形代数学をしっかり学んでいて欲しいです。さらに、代数学（群・環・体）の基礎について学んでいてくれると入学後に学びやすいはずです。（数学では珍しく）有限な対象を研究しているので、計算機（コンピュータ）による数値計算の経験があればさらに学びやすいです。
進学において、ご質問などありましたら、どうぞお気軽にメールでお問い合わせ下さい。
(B01-2) 船野研究室では、リーマン幾何学、スペクトル幾何学、バナッハ空間・距離空間の幾何学などの周辺分野を研究しています。
リーマン幾何学には空間の曲がり具合を表す概念である断面曲率、リッチ曲率、スカラー曲率があります。これらの曲率の下限の条件を課すことは、考えている空間をわかりやすい空間とある意味で比較することに対応することが知られています。比較幾何学ではこれらの比較を用いて考えている空間の幾何学的性質を調べます。バナッハ空間論ではタイプ・コタイプといった上の比較とは別のユークリッド空間との比較があります。近年これらの比較の概念は距離空間へと拡張され、ワイルドな空間の取り扱いが可能となってきました。近年凸幾何学における種々の方法がリッチ曲率が下に有界なリーマン多様体に拡張されてきており、凸幾何学とリッチ曲率の比較幾何学が密接に関係していることが示され始めてきました。今後の発展が期待される分野です。
ラプラシアンは最も基本的な二階楕円型偏微分作用素であり、偏微分方程式だけではなく幾何学でも様々な場面で現れます。熱方程式、波動方程式、シュレディンガー方程式などの解はラプラシアンの固有値並びに固有関数を用いて表されることが知られており、これら方程式の解の構造を理解するのにラプラシアンの固有値・固有関数の研究は大切になります。また曲率・体積・閉測地線の分布・等周問題などなど幾何学的量とも関係しています。離散的な取扱いにおいては、効率の良い経済的なネットワークの構成、クラスタリングの研究などの応用分野とも関係しています。近年では最適輸送理論や代数的位相幾何学などといった一見関係のないような分野の道具を駆使して研究を行っており新たな発展を目指しています。多様体を曲面のファミリーで掃き出し面積のミニマックスを考えると幅と呼ばれる幾何学的な量が現れますがこのような他のミニマックス理論の研究にも興味を持っています。
船野研究室では基本的に何を研究しても自由です、私のやってきた研究に沿う必要はなく自発的に色々なことに興味を持って勉強したり研究会やセミナーで話を聞いたりして自分の道を模索してみてください、迷った場合は遠慮せずに気軽に相談してください。幾何学といっても現在は幾何学のみで研究するのは難しく、解析学、確率論などの幾何学以外の分野も同時に勉強することになるかと思います。これら幅広い分野を効率よく勉強するには（優秀な）他人の話を聞いたり、相談・質問したりしてお互い協力し高め合うことが大切となります。遠慮せずにどんどん（数学の）相談・質問をしましょう！また私の研究室を選びたい場合は受験前になるべく早く私に（メールで）コンタクトをお願いします。
内藤 貫太 (Naito, Kanta)
教授
knaito@
根元 多佳子 (Nemoto, Takako)
准教授
nemototakako@
(B02-1) 内藤研究室では、関数推定や多変量解析の研究が行われています。
統計科学の多くの問題が関数の推定問題に要約されることが知られています。重要な問題として、密度関数や分布関数の推定、回帰関数やパターン認識における判別境界の推定が挙げられます。内藤研究室では、このような関数推定の問題に関する研究が積み上げられてきました。アルゴリズム主体の"機械学習"の手法を組み込んだ関数推定方法の開発も行ってきました。これからも、深層学習の手法を取り込んだ新しい関数推定の研究を進める予定です。
内藤研究室では、多変量データの解析方法の構築は自然に関数推定の問題と絡み合うことから、"多変量解析"についても研究の蓄積があります。"高次元"データ解析のための方法論の研究や理論的研究も含まれます。多様なデータの出現に応じて、新たな多変量データ解析手法の開発が求められます。そして、その手法の理論的な精度評価を行う研究も必要となるのです。
データ・サイエンティストになりたいのでしたら、大学院で統計科学の研究に携わるのが良いでしょう。特に、もし関数推定や多変量解析の研究に興味があるのでしたら、私まで是非お問い合わせください。
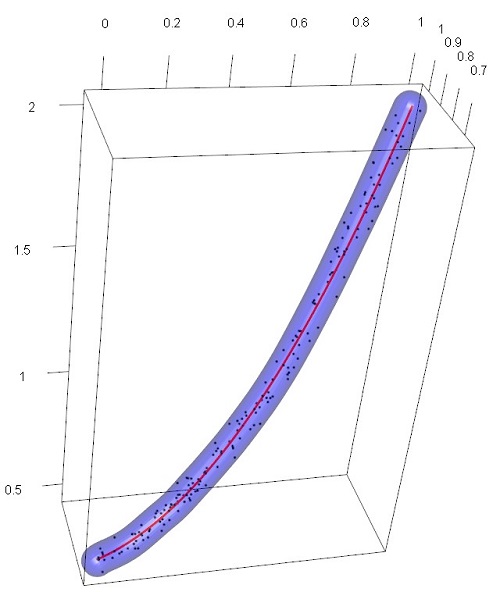
[3次元空間に埋め込まれた1次元曲線の同時信頼領域]
(B02-2) 根元研究室では、数理論理学、特に構成的数学などの分野を研究しています。
何かの定理を証明するときに、何をしてよいのか困ったことはありませんか？数学の定理の証明は「公理」から「推論」を組み合わせて導きます。公理とは証明抜きに真とされる仮定で、例えば群の公理は群が満たすべき条件をあげて、どういうものが群であるか規定します。「推論」とは何から何を帰結してよいのか規定する規則です。例えば「『AならばB』で、さらに『A』であるとき『B』と帰結してよい」三段論法は推論規則の一つです。数理論理学では、論理や証明、モデル、集合、計算といった数学で普段当たり前に使うものを対象として解析しています。私の研究はざっくりいうと「どんな公理とどんな推論規則を許したときに、何が帰結できるのか」を明らかにすることを目的としています。
普段はあまり意識することはないと思いますが、通常の数学の大半の定理ははZFC集合論と呼ばれる集合論の公理から古典論理と呼ばれる推論規則を使って証明されます。しかしこれが唯一の正しい公理と論理ではありません。例えば、真なる命題とは証明が与えられたものである、というモチベーションをもとに推論規則を組み立てると、未解決問題に対しては「AまたはAでない」が成り立つとは言えません。計算機で証明が書けるものを真と考えても同様のことが言え、このことは実際に自動証明や定理証明支援系の理論的なバックグラウンドになります。このように通常と違う推論を用いて数学をやってみると、普通の数学と大分違った世界が見えてきて、とても楽しいです。
数理論理学や構成的数学を学部で学んだことのある人は少ないと思いますが、証明やモデル、集合などが何なのか気になる人を歓迎します。研究テーマは各自の興味に沿って決めていきます。興味のある方は、メールにてお問合せください。
[2分木のパスの存在からの論理原理の証明]
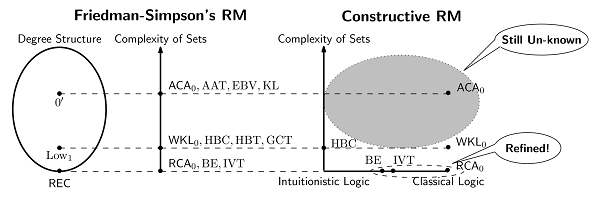
[構成的逆数学による数学の定理の分類]
荒木 由布子 (Araki, Yuko)
教授
yaraki@
Xin Guan (Guan, Xin)
特任助教
guan.xin.c5@
黄 傲 (Huang, Ao)
特任助教
統計数理学分野・荒木研究室では、統計数理学・データ解析分野の教育・研究を広くカバーしています。
近年の医療データ・人々の行動データ・経済データなどから、新しい価値をみいだし活用するAIや数理データサイエンスは飛躍的な発展をとげています。その発展を基盤・理論から支えるのが統計科学・統計数理学です。また逆に、AIや数理データサイエンスから得た発想・手法を活かして、統計科学・統計数理学の従来の課題を一気にブレイクスルーする新しいタイプの統計モデリングの構築もめざしています。主な研究分野は以下のとおりです。なお、詳細は研究室のWebページもご覧ください。
私たちの世界に存在するさまざまなデータは、規則性と同時に不確実性を有しバラツキます。この規則性と不確実性を、数学という科学の共通言語を使って把握し、データから効率的に有益な情報やパターンを抽出する学問が統計科学・統計数理学です。荒木研究室では、近年の高度に発展した測定技術で観測・測定され蓄積された、時間や空間の推移に伴い変化する複雑多様な構造をもつデータから、情報量の損失を最小限に抑えながら有益な情報を抽出するための、新たな統計モデルの開発を理論的・応用的両側面から研究しています。推定したモデルを評価するための新たなモデル選択規準を導出し、数値実験により手法の有用性を検証しています。有用性が検証された統計モデルは実データへ適用し、新たな知見の獲得を目指します。
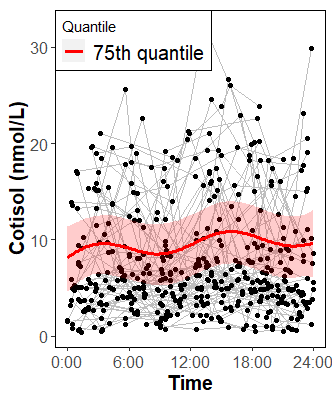
Longitudinal data of urinary cortisol
concentrations
and the estimated
75th quantile regression curve.
(Tanabe, Araki et al. 2022)
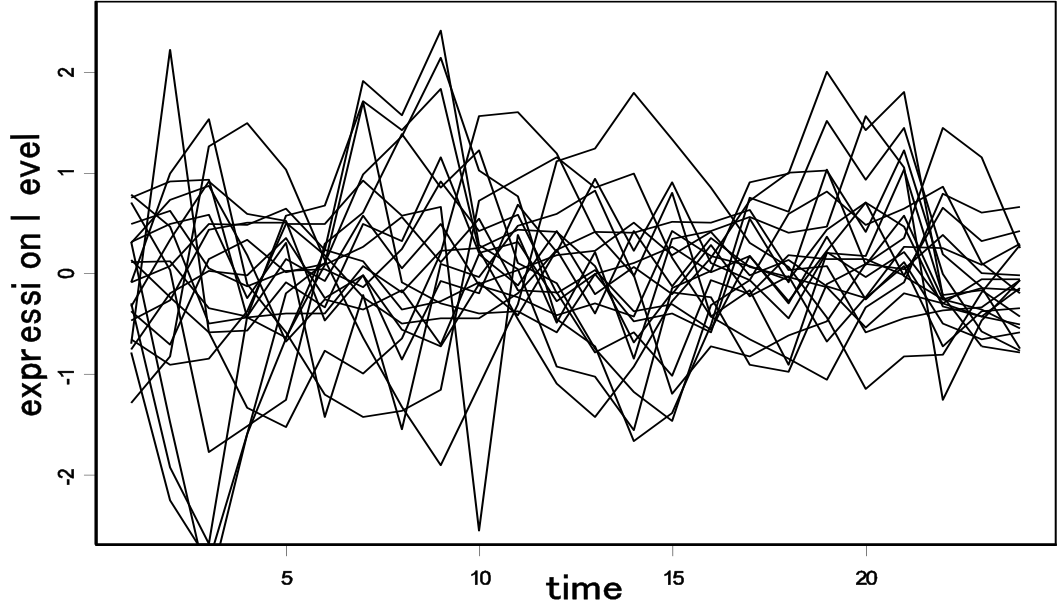
（左）経時的マイクロアレイデータ (Spellman et al. 1998)
（右）Expressions of genome-wide genes in the yeast genome using cDNA microarrays under CDC15 based synchronization. (Araki et al. 2009)
関数データ解析とは、各個体や対象に対して、離散点で経時的・空間的に観測・測定された一組の複雑な構造を有する高次元データ（p>>n）を滑らかな関数として捉え、関数化し次元縮小を行い、その関数化データの集合から有効に情報を抽出するための統計モデルの構築からなる一連の手法です。現在最も注目を集めている解析法の１つで、自然科学の様々な分野のデータに加え、 IoTデータ、MRI画像解析や運動機能解析データなどもターゲットです。
超高次元データの解析では、未知パラメータ数pが多大である一方、個体数nが限られているため、従来の手法では適切な次元縮小と安定した汎化能力の高い統計モデルのパラメータ推定が困難でした。その結果、諸科学の高次元データを扱う分析現場では、部分データや平均値による解析をはじめ、仮定の検討のない従来の統計モデルの適用など、結果の追求が最優先されている場合があります。また現在多用されている機械学習の各手法において、統計科学の観点からみると理論的基盤の確立と固有の評価指標の開発が必要なものも散見されます。
関数データ解析は、p>>n問題で従来の解析法が適用できない超高次元小標本データや複雑な非線形構造を有する高次元データでも次元縮小が可能で、さらに個体間で観測点数や位置が異なる場合でも適切な分析を可能とします。例えばArakiら(2019)は、関数化において、各個体(対象)に対して多数の離散点で測定された一組の高次元データの次元縮小のため、基底展開とスパース主成分分析による合成基底関数展開法を提案しました。さらに次のステップである関数データ解析に基づく統計モデル開発では、関数データを使って多変量解析を高次元データへ拡張した、関数多変量解析モデルを新たに構築しています。このとき、モデルのパラメータ推定を各段階で行う｢2段階法｣(推定方程式が簡便で計算量が少)と、2段階のパラメータを同時にベイズ推論により推定する｢ジョイント法｣(観測誤差・個体間変動が大きい場合にも有効)があります。
荒木研究室では、｢2段階法｣と｢ジョイント法｣を併用し、Jensen-Shannon情報量やベイズ型情報量に基づく情報量基準を構築し、モデルの設定・推定・評価を行う理論体系の確立と、関数データ解析による非線形多変量解析の体系化をめざしています。
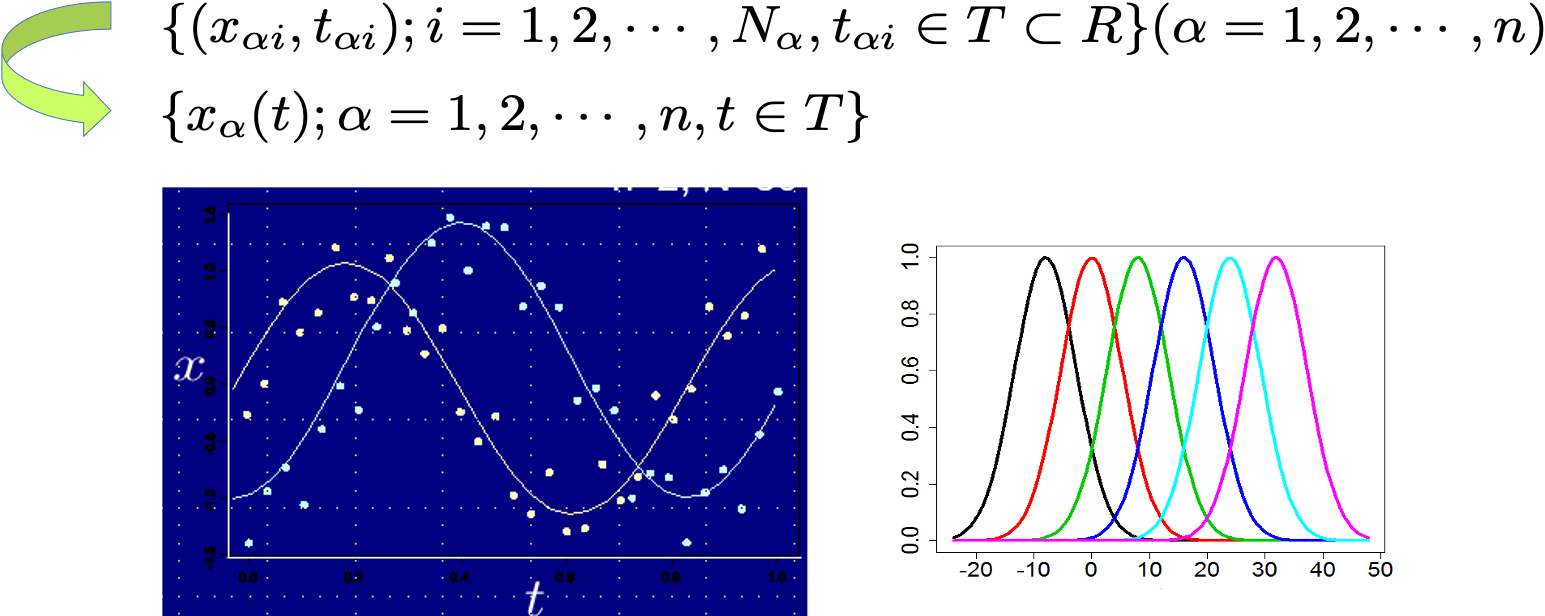
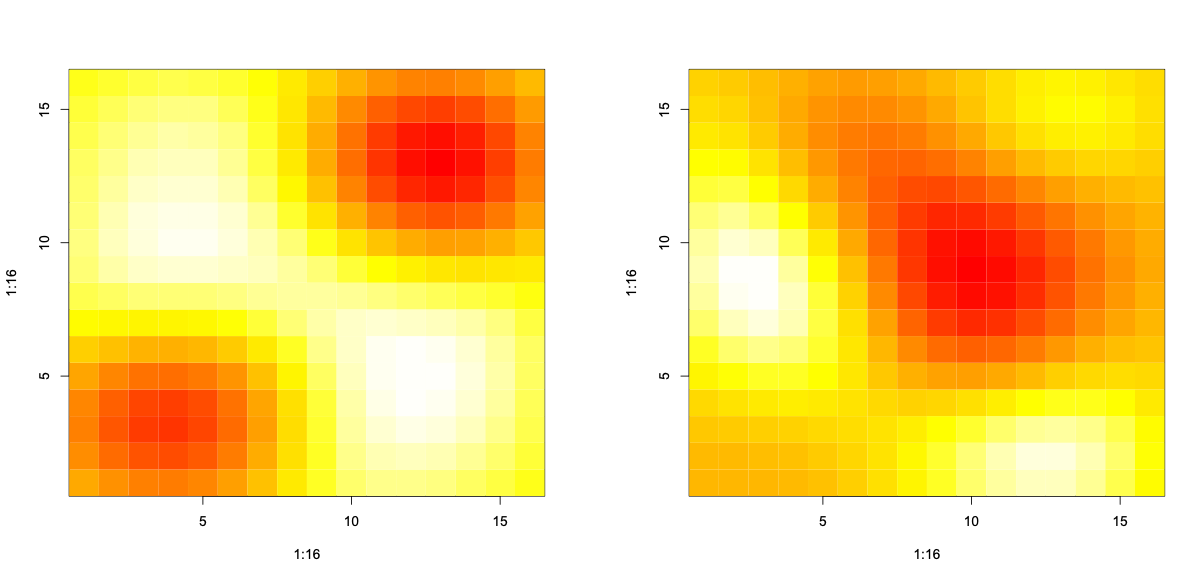
Composite basis functions
(Araki and Kawaguchi 2019)
ヒトのデータの不確定性を数理的に捉え、病気の診断や治療に関する決定を科学的根拠に基づき行うためのバイオ統計学の実践的研究に、学外の教育・研究機関や医療機関と研究者レベルで連携して取り組んでいます。
従来の健康管理制度による身体・血液検査値データや、近年の急速な観測・測定技術の進歩に伴い観測されるようになったNIRSやMRI画像の高次元データのための統計モデルの開発・分析を行っています。これらは例えば脳梗塞の危険予知などのために新しい知見を得ています。また長期・多項目について測定されたヒト個人の身体ダイナミックス・データを情報量を失うことなく関数データ化し、その関数データに凸クラスタリング手法を使って求めた群予測と個体の属性データ、身体ダイナミクスの関数データとともに生存時間解析モデルに組み込む新モデルの開発も行っています。
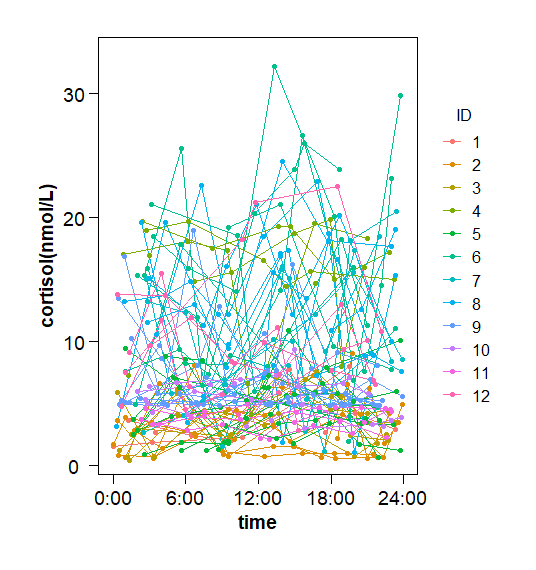
乳児コルチゾール分泌データ
(Tanabe, Araki et al. 2022)
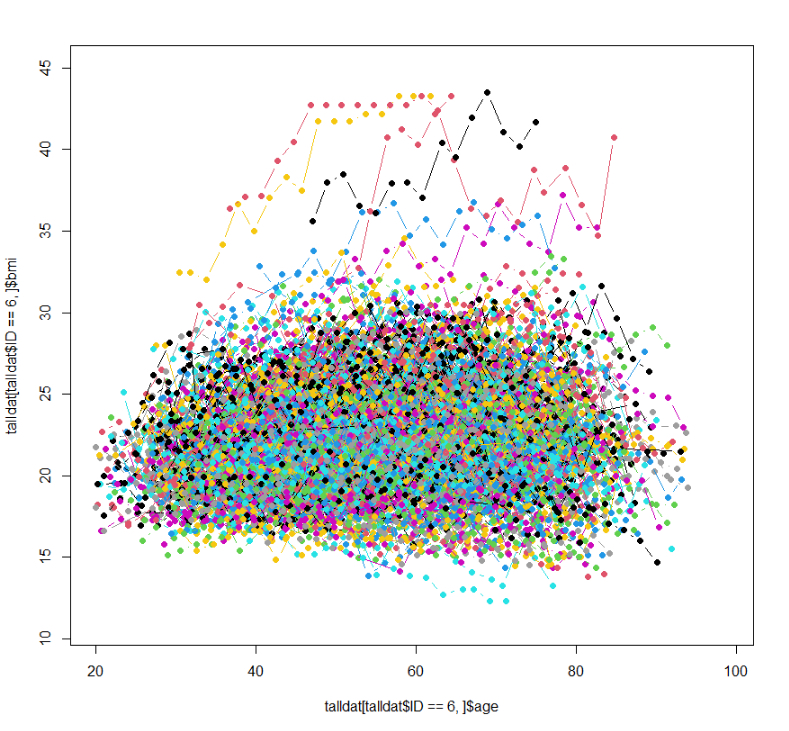
Female: BMI trajectories
修士研究として、皆さんが卒業研究として取り組んだ題目をさらに発展させることも可能です。
統計モデル・関数データ解析・機械学習
バイオ統計学
学習科学・スポーツデータ解析・その他
研究テーマは各自の興味に沿って決めていきますので、能動的な研究姿勢が求められます。道のないところに自ら道をつけていく、といった意気込みを持った方を歓迎します。統計科学の研究に興味を持った方は、メールにてお問い合わせください。
